Solve The Following System Of Equations Algebraically
Systems Of Equations Solved Algebraically
Solve the following system of equations algebraically. Solve the system using elimination. XXXy ax2 bx c. So we have the new system of equations.
The only variable that qualifies in this system is x in the first equation. Or click the example. Multiply the both sides of the second equation by -2.
Solve the following equation algebraically. X 3 y 4 and 2 x 5 y 5. XXXy 3x2 2x 4.
The easiest one perhaps is substitution method. Solve the following system of equations algebraically. Substitute the expression found in step 1 into the other equation.
There is no solution. Y x2 6x 5 y 7 2x 28. X2y11 Try it now.
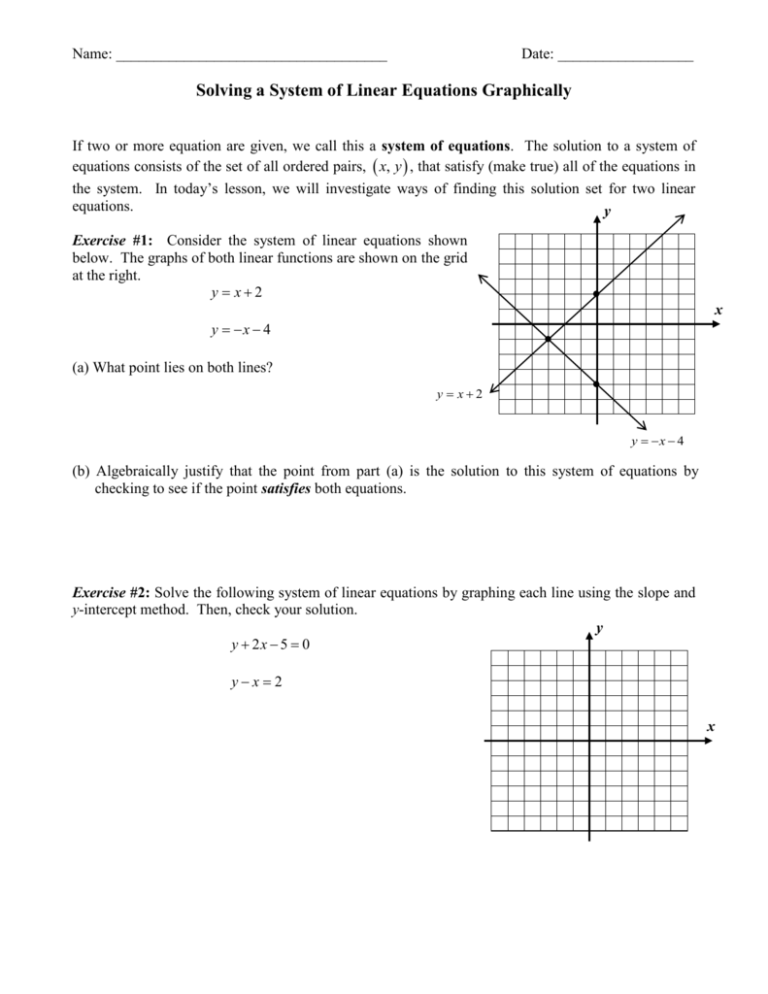
Solve the following system of equations. Start with the given system of equations. Then a comma Then the second equation x2y11.
9x² y² 9 3x y 3 Lets do it algebraically and then check it graphically. 4x y 11.
Solve Systems Of Equations Algebraically Youtube
Solving Linear Systems Algebraically Youtube
Systems Of Equations Solved Algebraically
Solved Solve The Following Systems Of Equations Chegg Com
Math 11 Sec 8 2 Solving Systems Of Equations Algebraically Youtube
Systems Of Equations Solved Algebraically
5 5 Solving Systems Of Equations Algebraically Youtube
Solving Systems Of Equations Ppt Video Online Download
How To Solve A System Of Equations Algebraically With The Elimination Method Youtube
Graphing Is Just One Way To Solve A System Of Equations Ppt Download
Systems Of Equations Solved Algebraically
Solving Systems Of Linear Equations Lesson Article Khan Academy
Solved Section A Show All Your Work Ar1 5 X 2 Marks Chegg Com
3 2 Solving Systems Algebraically When You Try To Solve A System Of Equations By Graphing The Coordinates Of The Point Of Intersection May Not Be Obvious Ppt Download
Answered 2 Using The Substitution Method Ken Bartleby
Solve Simultaneous Equations Algebraically Teaching Resources
Solving Systems Of Equations Ppt Video Online Download
Math 20 1 Chapter 8 Systems Of Equations
Solving Systems Of Equations Using Algebra Calculator Mathpapa
A19b Solving Two Linear Simultaneous Equations Graphically Or Algebraically By Substitution Bossmaths Com
Solved Solve The Following System Of Equations Chegg Com
Using The Substitution Method To Solve A System Of Equations
Math 20 1 Chapter 8 Systems Of Equations Ppt Video Online Download
1
8 Solving Systems Of Equations
Solving Systems Of Equations Algebraically Steps 1 Solve For A Variable In Either Equation Get Variable Alone X Or Y 2 Substitute For This Variable Ppt Download
How To Solve A System Of Equations Using Substitution
Solve The Following System Of Equations Algebraically Y X 2 3x 10 Y X 10 Brainly Com
Solved 6 Solve The Following Systems Of Equations Chegg Com
Using The Substitution Method To Solve A System Of Equations
Solving Systems Algebraically Both Methods Mr Williams Math Class
Answered Solve The Following Systems Of Bartleby
3 2 Solving Systems Algebraically Swbat 1 Solve Systems Of Linear Equations By Using Substitution 2 Solve Real World Problems By Using Systems Of Linear Ppt Download
Solved Solve The Following System Of Equations Algebraically Chegg Com
Solved Section A Show All Your Work Ar1 5 X 2 Marks Chegg Com
Simultaneous Equations Applying Algebraic Skills To Linear Equations I Can Solve Simultaneous Equations Graphically Solve Simultaneous Equations Algebraically Ppt Download
Solve The Following System Of Equations Algebraica Gauthmath
Solving A System Of Linear Equations Graphically
Math 20 1 Chapter 8 Systems Of Equations
Examview Aa10 Solvinglinearsystems2 Tst
Solving Linear Systems
Solve The Following System Of Equations Algebraically 4x 5y 18 3x 2y 10 Brainly Com
Simultaneous Equations Linear And Quadratic Worksheet
Solving Systems Of Equations By Elimination Video Khan Academy
Solving System Of Equations That Have 0 1 And Infinite Solutions Ppt Video Online Download
8 Solving Systems Of Equations
Math 20 1 Chapter 8 Systems Of Equations
Answered Using The Substitution Method Vito Is Bartleby
Solving Systems
The only variable that qualifies in this system is x in the first equation.
X B Y C. Solving a System of Two Linear Equations in Two Variables using Substitution. Show all your work. Tap again to see term. Solve the following system of equations algebraically. Solve for in second equation then substitute the second equation into the first. 2 3 B 2 - 2 B 8 Elimination Method. Try MathPapa Algebra Calculator. Example Click to view xy7.
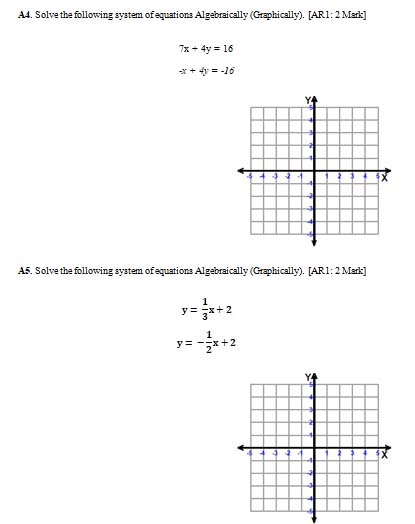
How many solutions does the following system of linear equations have and I have my system right over here theres a couple of ways to think about it one way is to think about them graphically and think about well are they the same line in which case they would have an infinite number of solutions are they parallel in which case they never intersect youd have no solutions or do they intersect exactly one place in. This video also includes special cases of systems without a. Solve the following system of equations algebraically and check. X B Y C. Click card to see definition. Both equations are in standard form. Solve the following system of equations algebraically.
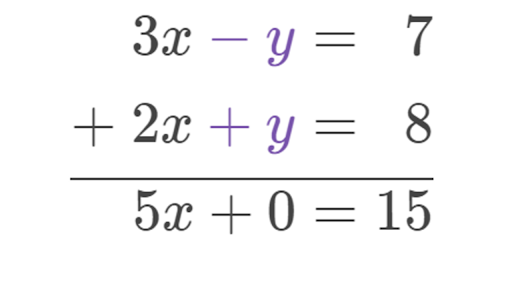
Post a Comment for "Solve The Following System Of Equations Algebraically"